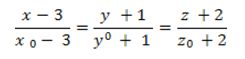LINGKARAN

           Definisi Lingkaran 
                   

                 Lingkaran adalah himpunan titik-titik (tempat kedudukan titik-titik) pada bidang datar yang berjarak sama ke sebuah titik tertentu. Titik tertentu tersebut disebut “Pusat Lingkaran”, dan jarak yang sama itu disebut”Jari-Jari Lingkaran”. Lingkaran yang berpusat di titik M dan berjari-jari r ditulis dengan lambang (M, r).

Perhatikan gambar  berikut, 

Lingkaran K = (M, r). Untuk memperoleh persamaan lingkaran K, dilakukan cara berikut: Ambil sebarang titik P pada K.

M1 = Proyeksi titik M pada sumbu x 

P1 = Proyeksi titik P pada sumbu x 

T = Proyeksi M pada sumbu PP1

Pada segitiga MPT (siku-siku di T), 

                       𝑀𝑇² + 𝑃𝑇² = 𝑀𝑃²

↔ 𝑀₁𝑃₁² + (𝑃𝑃₁ − 𝑇𝑃₁)² = 𝑀𝑃²

↔ (𝑂𝑃₁ − 𝑂𝑀₁)² + (𝑃𝑃₁ − 𝑀𝑀₁)² = 𝑀𝑃²

↔ (𝑥_𝑃 − 𝑥_𝑀)² + (𝑦_𝑃 − 𝑦_𝑀)² = 𝑅²

maka Jika koordinat titik P dijalankan, terdapatlah persamaan lingkaran K, yaitu:

𝐾 ∶ (𝑥 − 𝑥_𝑀)² + (𝑦 − 𝑦_𝑀)² = 𝑅²

Adalah persamaan lingkaran yang berpusat di titik M dan berjari-jari = R. Jika persamaan lingkaran K tersebut dijalankan maka dapat :

𝐾 ∶ (𝑥_𝑃 − 𝑥_𝑀)² + (𝑦_𝑃 − 𝑦_𝑀)² = 𝑅²

𝐾  ∶  𝑥² −  2𝑥_𝑀𝑥 +  𝑥²_𝑀 +  𝑦² −  2𝑦_𝑀𝑦 + 𝑦²_M− 𝑅² = 0

↔ 𝐾  ∶  𝑥²  +  𝑦²  −  2𝑥_𝑀𝑥  −  2𝑦_𝑀𝑦 +  𝑥²_𝑀 + 𝑦²_M− 𝑅² = 0

Jika − 2𝑥_𝑀 = 𝐴     − 2𝑦_𝑀 = 𝐵      dan      𝑥²_𝑀 + 𝑦²_M− 𝑅² = 𝐶

Maka persamaan lingkaran K menjadi :

𝐾 ∶ 𝑥² + 𝑦² + 𝐴𝑥 + 𝐵𝑦 + 𝐶 = 0

Read More

BOLA

         Definisi Bidang Bola 

Bidang bola atau bola adalah himpunan titik – titik (tempat kedudukan titik) pada R³ yang jaraknya sama terhadap sebuah titik tetep. Titik tetap itu adalah pusat bola. Dan jarak yang tetap itu disebuah berjari-jari bola. Bola dengan titik pusat M dan berjari-jari R ditulis dengan lambang (M,R) untuk memperoleh persamaan bola (M,R) dilakukan cara berikut.

Perhatikan gambar

Ambil sebarang titik P yang terletak pada bola K

M₁        : Proyeksi M pada xoy

P₁         : Proyeksi P pada xoy

M₂        : Proyeksi M₁ pada sumbu x

P₂         : Proyeksi P₁ pada sumbu x

S          : Proyeksi M pada PP₁

T          : Proyeksi M₁ pada PP₂

Pada ΔMPS (Siku-siku pada S)

Bila koordinat P dijalankan terdapatlah persamaan bola K (M,R)

Jika persamaan bola K(M,R) ini dijabarkan terdapatlah

Jadi Persamaan bola K (M,R)

Bidang singgung pada bola

Pada bola K terletak titik P, Jika persamaan bola K dan koordinat titik P telah diketahui, maka persamaan bidang bola K dengan titik singgungnya P tersebut iperoleh sebagai berikut :

      Jika V = bidang singgung pada bola K yang titik singgungnya adalah P, maka V tegak lurus garis MP Jadi V adalah bidang yang melalui titik P dengan bilangan arah Maka persamaan bidang V adalah :

      Maka persamaan bidang V adalah : 

P adalah titik yang terletak pada bola K, maka

Adalah persamaan bidang singgung pada bola K dengan titik P sebagai titik singgungnya

 Kuasa pada bola 

Melalui titik P yang terletak di luar bola K dibuat garis g yang memotong bola K di titik-titik S dan T. Definisi: Yang dimaksud dengan kuasa titik P terhadap bola K adalah PS.PT Tinjauan: Kuasa titik P terhadap bola K tersebut bernilai tetap. Artinya tidak bergantung pada posisi garis g yang melalui P tersebut.Perhatikan Gambar 3.7 Garis g melalui titik P, memotong bola K di titik-titik S dan T. Maka kuasa titik P terhadap bola K adalah PS.PT. 

Garis l melalui titik P, memotong bola K di titik-titik G dan H. Maka kuasa titi P terhadap bola K adalah PG.PH. Garis g dan l membentuk bidang W, yang memotong bola K pada lingkaran x.

Titik-titik S,T,G, dan H terletak pada lingkaran x, Maka ΔPTG ∞ ΔPHS

Jadi PG : PT = PS : PH atau PG . PH = PS . PT

Berarti kuasa titik P terhadap bola K bernilai tetap (tidak bergantung pada posisi garis g yang melalui P)

Read More

TUGAS  4 

Read More

BIDANG KERUCUT

Pengertian Bidang Kerucut

    Pandang suatu garis lengkung yang termuat pada bidang V dan ada di titik P di luar  bidang V. Garis-garis yang ditarik melalui P dan titik-titik pada kurva itu membentuk suatu himpunan garis lurus yang merupakan bidang lengkung. Bidang lengkung yang terjadi disebut bidang kerucut yang selanjutnya disebut kerucut.

Perhatikan ilustrasi berikut : Misalkan k (garis lengkung dasar) terletak pada bidang V dan titik P di luar bidang V. kemudian lukis garis-garis melalui titik P dan titik pada k. Garis-garis tersebut akan membentuk suatu himpunan yan merupakan sebuah bidang lengkung seperti di bawah ini. Bidang lengkung yang terjadi adalah Bidang Kerucut.

         

                             

Kemudian pandang jika k merupakan sebuah lingkaran dan P terletak sebarang di luar V. Dengan cara yang sama seperti di atas, maka diperoleh sebuah bidang lengkung. Bidang lengkung yang terjadi disebut Kerucut Lingkaran Miring.

  

      

Sekarang pandang jika k merupakan sebuah dan proyeksi P terhadap V berimpit dengan pusat lingkaran. Dengan cara yang sama dengan di atas maka diperoleh sebuah bidang di atas maka diperoleh sebuah bidang lengkung yang disebut kerucut Lingkaran Tegak.

      Persamaan Bidang Kerucut 

Untuk menentukan persamaan bidang kerucut, dilakukan dengan cara sebagai berikut : Misalkan, diketahui persamaan garis lengkung dasar kerucut adalah 

dan puncak P(x₁, y_1, z₁)

Tentukanlah persamaan kerucut tersebut. Ambil sebarang titik 

pada garis lengkung k. ini berarti :

Sedangkan persamaan garis pelukis kerucut adalah persamaan garis yang melalui titik T dan P yaitu :

        Persamaan bidang kerucut diperoleh jika titik  dijalankan sepanjang kurva k. Artinya kita eliminasi  dan  dari persamaan 1, 2, 3.

Contoh :

Tentukan persamaan kerucut dengan puncak P(3, -1, -2) dan persamaan garis lengkung dasarnya adalah :

Jawab :

Ambil titik T(x_₀, y_₀, z_₀) sebarang pada garis lengkung dasar S. Ini berarti :

Kemudian persamaan garis pelukisnya adalah persamaan garis yang melalui  dan P(3, -1, -2)  adalah :

Persamaan bidang kerucut diperoleh jika koordinat titik T dijalankan. Artinya kita eliminasi  dan  dari persamaan (1), (2), dan (3)

Persamaan di atas dapat dinyatakan dalam bentuk :

Subsitusikan persamaan (3) ke persamaan (2), maka diperoleh :

Kemudian subsitusikan persamaan (3) dan persamaan (4) ke persamaan (1)

untuk

Berdasarkan (*) maka diperoleh persamaan kerucut yang diminta adalah :

Irisan Kerucut

Irisan kerucut adalah tempat kedudukan titik-titik sedemikian hingga perbandingan jarak titik ke suatu titik tertentu dan garis tertentu tetap harganya.

Perhatikan gambar 8, jika garis  I dan g berpotongan di titik O dan membentuk sudut sebesar . Jika garis I diputar mengelilingi garis g dengan besar sudut tetap maka lintasan hasil perputaran berupa kerucut lingkaran tegak. Garis g disebut garis sumbu dan garis I disebut garis pelukis, titik O disebut titik puncak kerucut dan disebut setengah sudut puncak.

Jika ada sebuah bidang V (bidang iris) memotong kerucut dengan membentuk sudut sebesar Y maka ada tujuh kemungkinan bentuk irisan bidang V dengan kerucut tersebut. 

1.    Jika bidang iris (penampang) melalui titik puncak O maka mempunyai kemungkinan:              

                         i.     Y >  irisannya berupa titik

                       ii.     Y >  irisannya berupa 2 garis berpotongan

                     iii.     Y =  irisannya berupa sebuah garis singgung

2.    Jika bidang iris (penampang) memotong kerucut tidak pada puncak maka mempunyai kemungkinan:

                        i.     Y = 90^oirisannya berupa lingkaran

                      ii.     Y =  irisannya berupa parabola

                    iii.     Y >  irisannya berupa elips

                    iv.     Y <  irisannya berupa hiperbola

Jika irisan kerucut ditinjau secara analitis maka irisan kerucut adalah tempat kedudukan himpunan titik yang perbandingan jarak titik tersebut dengan titik tertentu dan garis tertentu tetap nilainya. Nilai tetap ini selanjutnya disebut eksentrisitas dan disingkat e. Kemungkinan-kemungkinan irisan kerucut yang terjadi ditinjau dari nilai e adalah:

e = 1 maka irisan berupa parabola

0 < e < 1 maka irisan berupa elips

e > 1 maka irisan berupa hiperbola

e = 0 maka irisan berupa lingkaran

Contoh :

Carilah persamaan irisan kerucut dengan direktrik  2x - 3y + 6 fokusnya F(-1, -2) dan eksentrisitasnya e = 1

Jawab :

1.      Ambil sebarang titik pada irisan kerucut misal A( X_A, Y_A)

2.      Jarak A ke garis direktrik dengan P titik pada garis direktrik

Koordinat titik A dijalankan didapat

Jadi persamaan irisan kerucut dengan direktrik  2x - 3y + 6 fokusnya F(-1, -2) dan eksentrisitasnya e = 1 adalah 

Read More